THIS IS B3c0me

记录生活中的点点滴滴

0%

迁移学习

发表于 分类于

什么是迁移学习

​ 迁移学习，简单来讲就是机器能够“举一反三”，例如本来能够分辨猫和狗的神经网络在经过少量的训练后能够很好地分辨老虎和狮子，这就叫迁移学习。迁移学习可以将在一个领域训练的机器学习模型应用到另一个领域，在某种程度上提高了训练模型的利用率，解决了数据缺失的问题。迁移学习使不依赖于大数据的深度学习成为可能。

​ 有了迁移学习，我们便可以将神经网络像软件模块一样进行拼装和重复利用。例如，而我们可以将在大数据集上训练好的大型网络迁移到小数据集上，从而只需经过少量的训练就能达到良好的效果。我们也可以将两个神经网络同时迁移过来，组成一个新的网络，这两个神经网络就像软件模块一样被组合了起来。

迁移学习的由来

​ 监督学习要求训练集和测试集上的数据具有相同的分布特性。而迁移学习允许训练集和测试集的数据有不同的分布、目标甚至领域。

迁移学习的意义

​ 未来，随着迁移学习的大量应用，可能会出现一种新的商业形态：大公司运用大数据训练大模型，再将这些模型迁移到小公司擅长的特定垂直领域中。以语音识别为例：大公司可以运用大规模语料训练打的语音识别模型，这种模型在99%的日常应用场景中能达到很高的准确度，但是对于一个充斥着大量专业术语的学术会议的情景，这种通用的语音识别模型可能识别98%的常用词汇，但是另外2%的学术术语反而是这个学术会议的关键。在这种情境下，如果结合大语音识别模型，运用迁移学习技术，再去训练一个专门针对数学领域的语音识别模型，则有可能实现关键性的突破。

运用神经网络实现迁移学习

​ 深度神经网络会在不同的层学到数据中不同尺度的信息，所以可以将不同的层视作不同尺度的特征提取器。

​ 迁移学习方式一般可分为预训练模式和固定值模式：

  • 预训练模式：将迁移过来的权重视作新网络的初始权重，在训练的过程中会被梯度下降算法改变数值。
  • 固定值模式：迁移过来的部分网络在结构和权重上都保持固定的数值，训练过程进针对迁移模块后面的全连接网络

​ 其中固定值模式需要调节的参数少，学习的收敛速度理论上会更快。我们应根据实际问题的需要选择使用更适合的迁移学习模式。

迁移大型卷积神经网络：

——蚂蚁还是蜜蜂

下面我们动手实现迁移学习：区分画面上的动物是蚂蚁还是蜜蜂

ResNet与模型迁移

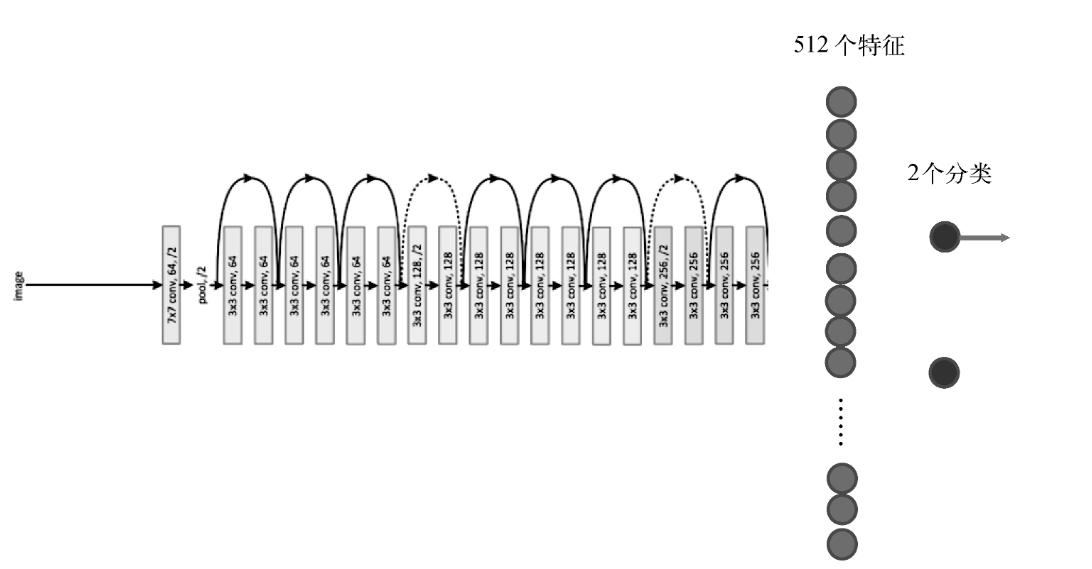
​ 我们迁移一个18层的残差网络精简版（ResNet）。残差网络是一种特殊的卷积神经网络，有152层，在物体分类等任务上具有较高的准确度。

​ pytorch提供多种层数（18/34/50/101/152）的ResNet模型，都已经是在ImageNet数据集上训练完毕的网络，因此可以直接拿来进行迁移学习。

​ 我们的新模型是一个深层的ResNet与两层全连接的组合。如下图所示：

代码实现

以下分别用预训练和固定值方式对这个深度网络进行训练：

  • 导入所有需要的包
1
2
3
4
5
6
7
8
9
10
11
12
#加载程序所需要的包
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
import torchvision
from torchvision import datasets, models, transforms
import matplotlib.pyplot as plt
import time
import copy
import os
  • 加载需要的数据
一、加载数据

运用PyTorch的dataset来加载硬盘上的大量图像
只要我们将大量的图像文件都放入指定的文件夹下（训练数据集在data/train下面，校验数据集在data/val下面）
并且将不同的类别分别放到不同的文件夹下。例如在这个例子中，我们有两个类别：bees和ants，我就需要在硬盘上
建立两个文件夹：bees和ants。

我们只需将相应的训练数据和校验数据图像放到这两个文件夹下就可以用datasets的ImageFolder方法自动加载

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 从硬盘文件夹中加载图像数据集

# 数据存储总路径
data_dir = 'data'
# 图像的大小为224*224
image_size = 224
# 从data_dir/train加载文件
# 加载的过程将会对图像自动作如下的图像增强操作：
# 1. 随机从原始图像中切下来一块224*224大小的区域
# 2. 随机水平翻转图像
# 3. 将图像的色彩数值标准化
train_dataset = datasets.ImageFolder(os.path.join(data_dir, 'train'),  #  将目标文件的路径加载到系统 data/train
                                    transforms.Compose([ 
                                        transforms.RandomResizedCrop(image_size),  # 随机裁取大小图片
                                        transforms.RandomHorizontalFlip(),  # 以给定的概率随机水平旋转给定的图像，默认为0.5
                                        transforms.ToTensor(),  # 将图片数据转换为张量
                                        #对图像进行归一化处理。其中[0.485, 0.456, 0.406]是图像的均值，[0.229, 0.224, 0.225]是图像的标准差。
                                        transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])  # 
                                    ])
                                    )

# 加载校验数据集，对每个加载的数据进行如下处理：
# 1. 放大到256*256像素
# 2. 从中心区域切割下224*224大小的图像区域
# 3. 将图像的色彩数值标准化
val_dataset = datasets.ImageFolder(os.path.join(data_dir, 'val'),
                                    transforms.Compose([
                                        transforms.Resize(256),
                                        transforms.CenterCrop(image_size),  #  从中心区域切割
                                        transforms.ToTensor(),
                                        transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
                                    ])
                                    )

# 创建相应的数据加载器
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size = 4, shuffle = True, num_workers=4)  # 4线程
val_loader = torch.utils.data.DataLoader(val_dataset, batch_size = 4, shuffle = True, num_workers=4)

# 读取得出数据中的分类类别数
num_classes = len(train_dataset.classes)

# 检测本机器是否安装GPU，将检测结果记录在布尔变量use_cuda中
use_cuda = torch.cuda.is_available()

# 当可用GPU的时候，将新建立的张量自动加载到GPU中
dtype = torch.cuda.FloatTensor if use_cuda else torch.FloatTensor
itype = torch.cuda.LongTensor if use_cuda else torch.LongTensor
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def imshow(inp, title=None):
    # 将一张图打印显示出来，inp为一个张量，title为显示在图像上的文字
    
    #一般的张量格式为：channels*image_width*image_height
    #而一般的图像为image_width*image_height*channels所以，需要将channels转换到最后一个维度
    inp = inp.numpy().transpose((1, 2, 0))  
    
    #由于在读入图像的时候所有图像的色彩都标准化了，因此我们需要先调回去
    mean = np.array([0.485, 0.456, 0.406])
    std = np.array([0.229, 0.224, 0.225])
    inp = std * inp + mean
    inp = np.clip(inp, 0, 1)  # inp是输入的数组，0 1 分别是最大值和最小值
    
    #将图像绘制出来
    plt.imshow(inp)
    if title is not None:
        plt.title(title)
    plt.pause(0.001)  # 暂停一会是为了能够将图像显示出来。


#获取第一个图像batch和标签
images, labels = next(iter(train_loader))

# 将这个batch中的图像制成表格绘制出来
out = torchvision.utils.make_grid(images)

imshow(out, title=[train_dataset.classes[x] for x in labels])

运行的效果如下：

二、加载一个卷积神经网络作为对比
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
# 用于手写数字识别的卷积神经网络
depth = [4, 8]
class ConvNet(nn.Module):
    def __init__(self):
        super(ConvNet, self).__init__()
        self.conv1 = nn.Conv2d(3, 4, 5, padding = 2) #输入通道为3，输出通道为4，窗口大小为5，padding为2
        self.pool = nn.MaxPool2d(2, 2) #一个窗口为2*2的pooling运算
        self.conv2 = nn.Conv2d(depth[0], depth[1], 5, padding = 2) #第二层卷积，输入通道为depth[0], 输出通道为depth[1]，窗口为15，padding为2
        self.fc1 = nn.Linear(image_size // 4 * image_size // 4 * depth[1] , 512) #一个线性连接层，输入尺寸为最后一层立方体的平铺，输出层512个节点
        self.fc2 = nn.Linear(512, num_classes) #最后一层线性分类单元，输入为

    def forward(self, x):
        #神经网络完成一步前馈运算的过程，从输入到输出
        x = F.relu(self.conv1(x))
        x = self.pool(x)
        x = F.relu(self.conv2(x))
        x = self.pool(x)
        # 将立体的Tensor全部转换成一维的Tensor。两次pooling操作，所以图像维度减少了1/4
        x = x.view(-1, image_size // 4 * image_size // 4 * depth[1])
        x = F.relu(self.fc1(x)) #全链接，激活函数
        x = F.dropout(x, training=self.training) #以默认为0.5的概率对这一层进行dropout操作
        x = self.fc2(x) #全链接，激活函数
        x = F.log_softmax(x, dim=1) #log_softmax可以理解为概率对数值
        return x
    
    def retrieve_features(self, x):
        #提取卷积神经网络的特征图的函数，返回feature_map1, feature_map2为前两层卷积层的特征图
        feature_map1 = F.relu(self.conv1(x))
        x = self.pool(feature_map1)
        feature_map2 = F.relu(self.conv2(x))
        return (feature_map1, feature_map2)
def rightness(predictions, labels):
    """计算预测错误率的函数，其中predictions是模型给出的一组预测结果，batch_size行10列的矩阵，labels是数据之中的正确答案"""
    pred = torch.max(predictions.data, 1)[1] # 对于任意一行（一个样本）的输出值的第1个维度，求最大，得到每一行的最大元素的下标
    rights = pred.eq(labels.data.view_as(pred)).sum() #将下标与labels中包含的类别进行比较，并累计得到比较正确的数量
    # rights装到cpu中，以便后面打印出来   --hq20200726
    rights = rights.cpu() if rights.is_cuda else rights
    return rights, len(labels) #返回正确的数量和这一次一共比较了多少元素

# 加载网络
net = ConvNet()
# 如果有GPU就把网络加载到GPU中
net = net.cuda() if use_cuda else net
criterion = nn.CrossEntropyLoss() #Loss函数的定义 交叉熵
optimizer = optim.SGD(net.parameters(), lr = 0.0001, momentum=0.9)

record = [] #记录准确率等数值的容器

#开始训练循环
num_epochs = 20
net.train(True) # 给网络模型做标记，标志说模型在训练集上训练
best_model = net
best_r = 0.0
for epoch in range(num_epochs):
    #optimizer = exp_lr_scheduler(optimizer, epoch)
    train_rights = [] #记录训练数据集准确率的容器
    train_losses = []
    for batch_idx, (data, target) in enumerate(train_loader):  #针对容器中的每一个批进行循环
        data, target = data.clone().detach().requires_grad_(True), target.clone().detach()#data为图像，target为标签
        # 如果有GPU就把数据加载到GPU上
        if use_cuda:
            data, target = data.cuda(), target.cuda()
        output = net(data) #完成一次预测
        loss = criterion(output, target) #计算误差
        optimizer.zero_grad() #清空梯度
        loss.backward() #反向传播
        optimizer.step() #一步随机梯度下降
        right = rightness(output, target) #计算准确率所需数值，返回正确的数值为（正确样例数，总样本数）
        train_rights.append(right) #将计算结果装到列表容器中
        #因为所有计算都在GPU中，打印的数据再加载到CPU中
        loss = loss.cpu() if use_cuda else loss
        train_losses.append(loss.data.numpy())

    
     #train_r为一个二元组，分别记录训练集中分类正确的数量和该集合中总的样本数
    train_r = (sum([tup[0] for tup in train_rights]), sum([tup[1] for tup in train_rights]))
    #在测试集上分批运行，并计算总的正确率
    net.eval() #标志模型当前为运行阶段
    test_loss = 0
    correct = 0
    vals = []
    #对测试数据集进行循环
    for data, target in val_loader:
        data, target = data.clone().detach().requires_grad_(False), target.clone().detach()
        # 如果GPU可用，就把数据加载到GPU中
        if use_cuda:
            data, target = data.cuda(), target.cuda()
        output = net(data) #将特征数据喂入网络，得到分类的输出
        val = rightness(output, target) #获得正确样本数以及总样本数
        vals.append(val) #记录结果

    #计算准确率
    val_r = (sum([tup[0] for tup in vals]), sum([tup[1] for tup in vals]))
    val_ratio = 1.0*val_r[0]/val_r[1]
    
    if val_ratio > best_r:
        best_r = val_ratio
        best_model = copy.deepcopy(net)
    #打印准确率等数值，其中正确率为本训练周期Epoch开始后到目前撮的正确率的平均值
    print('训练周期: {} \tLoss: {:.6f}\t训练正确率: {:.2f}%, 校验正确率: {:.2f}%'.format(
        epoch, np.mean(train_losses), 100. * train_r[0].numpy() / train_r[1], 100. * val_r[0].numpy()/val_r[1]))       
    record.append([np.mean(train_losses), train_r[0].numpy() / train_r[1], val_r[0].numpy()/val_r[1]])

运行结果：

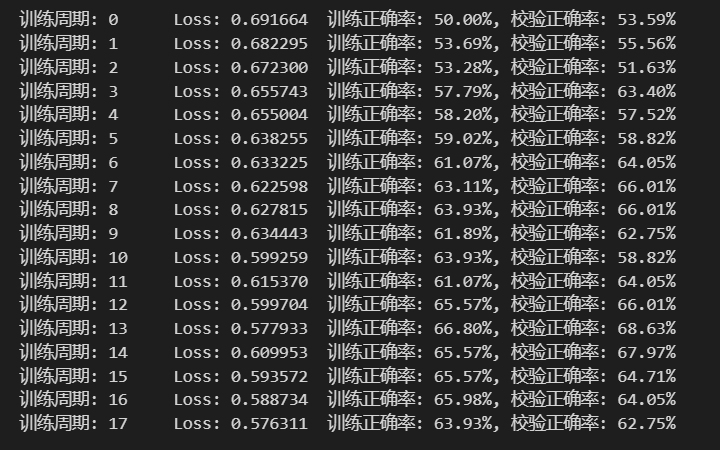
在测试集上分批运行，并计算总的正确率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#在测试集上分批运行，并计算总的正确率
net.eval() #标志模型当前为运行阶段
test_loss = 0
correct = 0
vals = []

#对测试数据集进行循环
for data, target in val_loader:
    data, target = data.clone().detach().requires_grad_(False), target.clone().detach()
    if use_cuda:
        data, target = data.cuda(), target.cuda()
    output = net(data) #将特征数据喂入网络，得到分类的输出
    val = rightness(output, target) #获得正确样本数以及总样本数
    vals.append(val) #记录结果

#计算准确率
rights = (sum([tup[0] for tup in vals]), sum([tup[1] for tup in vals]))
right_rate = 1.0 * rights[0].numpy() / rights[1]
right_rate

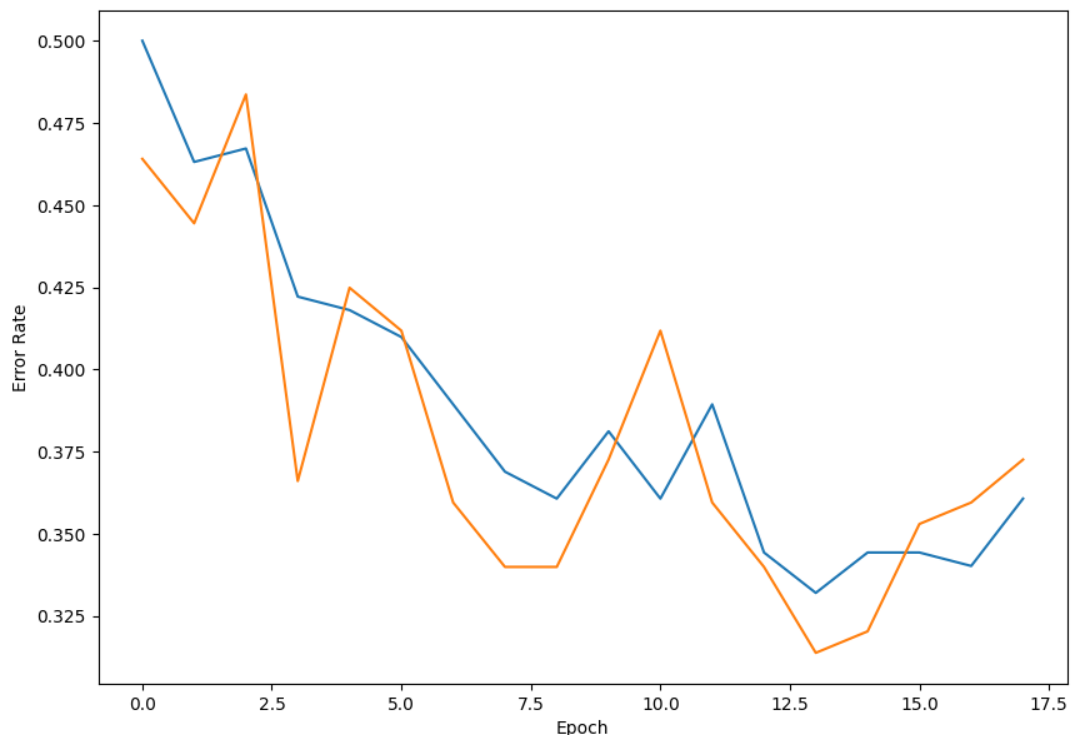
绘制误差率曲线：

1
2
3
4
5
6
7
8
9
10
# 绘制误差率曲线
x = [x[0] for x in record]
y = [1 - x[1] for x in record]
z = [1 - x[2] for x in record]
#plt.plot(x)
plt.figure(figsize = (10, 7))
plt.plot(y)
plt.plot(z)
plt.xlabel('Epoch')
plt.ylabel('Error Rate')

运行结果：

欢迎关注我的其它发布渠道