THIS IS B3c0me

记录生活中的点点滴滴

0%

Pytorch

发表于 更新于 分类于

“DO NOT GO GENTLE IN THE DARK”

不知不觉又踏入了人工智能的领域

在这里提醒自己不要忘了学习的初衷： 一切为安全

希望能够将学习到的人工智能方面的知识，包括深度学习、神经网络等应用到网络安全领域

回归问题实例

思路梳理：

  • 初始化学习参数：

    • learning_rate = 0.0001 #学习率

    • initial_b = 0 #初始b值

    • initial_w = 0 #初始w值

    • num_iterations = 10000 #迭代次数

    • points [x, y] #使用的点数据

  • 计算初始数据的损失

    • compute_error_for_line_given_points(initial_b, initial_w …)

  • 梯度下降计算

    • gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
      • step_gradient(b, w, np.array(points), learning_rate)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np

#linier aggression
#comupte the Loss Function
def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i ,1]
        totalError += (y - (w * x + b)) ** 2
    return totalError / float(len((points)))

#step_gradient, compute gradient steply
def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
        w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

#梯度下降循环运算
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    for i in range(num_iterations):
        b ,m = step_gradient(b, w, np.array(points), learning_rate)

    return [b, w]

def run():
    points = np.genfromtxt("data.csv", delimiter=",")
    learning_rate = 0.0001
    initial_b = 0
    initial_w = 0
    num_iterations = 10000
    print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
          .format(initial_b, initial_w, compute_error_for_line_given_points(initial_b, initial_w, points))
          )
    print("Running...")
    [b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
    print("After {0} iterations b ={1} , w={2}, error = {3}".
          format(num_iterations, b, w, compute_error_for_line_given_points(b, w, points))
          )

if __name__ == '__main__':
    run()
代码备注：

  • “data.csv”使用np生成的一个x,y坐标数据，生成代码如下：

    • np.random.rand() 生成的数据服从均值为0，方差为1的正态分布
    1
    2
    3
    4
    5
    6
    with open("data.csv", "w", newline="") as file:
        writer = csv.writer(file)
        for i in range(100):
            x = np.random.rand() * 100
            y = np.random.rand() * 100
            writer.writerow([x, y])

Tensor

torch.FloatTensor

用于生成数据类型为浮点的tensor，入参可以是列表，也可以是一个维度值

torch.range(起始值，结束值，步长)

搭建一个简易的神经网络

  • 简介：
1
2
1.设置输入节点为1000，隐藏层的节点为100，输出层的节点为10
2.输入100个具有1000个特征的数据，经过隐藏层后变成100个具有10个分类结果的特征，然后将得到的结果后向传播
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
batch_n = 100 #一个批次输入的数据量
hidden_layer = 100 #隐藏层的节点个数
input_data = 1000 #每个数据的特征为1000
output_data = 10 #输出具有是个分类结果的特征
# torch.set_printoptions(threshold=np.inf) #用于解决输出中省略号的问题
x = torch.randn(batch_n, input_data)
y = torch.randn(batch_n, output_data)

w1 = torch.randn(input_data, hidden_layer)
w2 = torch.randn(hidden_layer, output_data)

epoch_n = 20
lr = 1e-6

for epoch in range(epoch_n):
    h1 = x.mm(w1) #第一层权重计算
    print(h1.shape)
    h1 = h1.clamp(min=0)
    y_pred = h1.mm(w2) #第二层权重计算：预计输出值

    loss = (y_pred - y).pow(2).sum()
    print("epoch:{},loss{:.4f}".format(epoch, loss))

    grad_y_pred = 2 * (y_pred - y) #
    grad_w2 = h1.t().mm(grad_y_pred)

    grad_h = grad_y_pred.clone()
    grad_h = grad_h.mm(w2.t())
    grad_h.clamp(min=0)
    grad_w1 = x.t().mm(grad_h)

    w1 = w1 - lr * grad_w1
    w2 = w2 - lr * grad_w2

搭建一个较完整的神经网络

  • 代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    batch_n = 100  # 输入的数据量
    input_data = 1000  # 每个数据的特征数量
    hidden_layer = 100  # 隐藏层的神经元数量
    output_data = 10  # 输出为的特征量的个数

    '''
    自动梯度的功能过程大致为：先通过输入的Tensor数据类型的变量在神经网络的前向传播过程中生成一张计算图,
    然后根据这个计算图和输出结果精确计算出每一个参数需要更新的梯度，并通过完成后向传播完成对参数的梯度更新。
    完成自动梯度需要用到的torch.autograd包中的Variable类对我们定义的Tensor数据类型变量进行封装，
    在封装后，计算图中的各个节点就是一个Variable对象，这样才能应用自动梯度的功能。
    '''

    '''
    #用Variable对Tensor数据类型变量进行封装的操作。
    requires_grad如果是False，表示该变量在进行自动梯度计算的过程中不会保留梯度值。
    '''
    x = Variable(torch.randn(batch_n, input_data), requires_grad=False)
    y = Variable(torch.randn(batch_n, output_data), requires_grad=False)

    w1 = Variable(torch.randn(input_data, hidden_layer), requires_grad=True)
    w2 = Variable(torch.randn(hidden_layer, output_data), requires_grad=True)

    epoch_n = 50  # 迭代次数
    lr = 1e-6  # 学习率

    for epoch in range(epoch_n):
        h1 = x.mm(w1)  # 隐藏网络的净活性
        print(h1.shape)
        h1 = h1.clamp(min=0)
        y_pred = h1.mm(w2)  # 预计的输出值 也是隐藏网络的活性值

        loss = (y_pred - y).pow(2).sum()  # 损失函数
        print("epoch:{},loss:{:.4f}".format(epoch, loss))

        loss.backward()  # 后向传播

        w1.data -= lr * w1.grad.data
        w2.data -= lr * w2.grad.data

        w1.grad.data.zero_()
        w2.grad.data.zero_()

torch.nn.Sequential类

  • 备注：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
'''
torch.nn.Sequential类
是torch.nn中的一种序列容器
通过在容器中嵌套各种实现神经网络模型的搭建，
最主要的是，参数会按照我们定义好的序列自动传递下去
'''


'''
torch.nn.Sequential括号内就是我们搭建的神经网络模型的具体结构
Linear完成从隐藏层到输出层的线性变换，再用ReLU激活函数激活
torch.nn.Sequential类是torch.nn中的一种序列容器，通过在容器中嵌套各种实现神经网络模型的搭建，
最主要的是，参数会按照我们定义好的序列自动传递下去。
'''

'''
   torch.nn.Linear:
       torch.nn.Linear类用于定义模型的线性层，即完成前面提到的不同的层之间的线性变换。
        线性层接受的参数有3个：分别是输入特征数、输出特征数、是否使用偏置，默认为True
        使用torch.nn.Linear类，会自动生成对应维度的权重参数和偏置，对于生成的权重参数和偏置，我们的模型默认使用一种比之前的简单随机方式更好的参数初始化方式。
   torch.nn.ReLU:
        torch.nn.ReLU属于非线性激活分类，在定义时默认不需要传入参数。
        当然，在torch.nn包中还有许多非线性激活函数类可供选择，比如PReLU、LeaKyReLU、Tanh、Sigmoid、Softmax等
  
  '''

  • 代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    batch_n = 100  # 输入的数据量
    input_data = 1000  # 每个数据的特征数量
    hidden_layer = 100  # 隐藏层的神经元数量
    output_data = 10  # 输出为的特征量的个数

    x = Variable(torch.randn(batch_n, input_data), requires_grad=False)
    y = Variable(torch.randn(batch_n, output_data), requires_grad=False)
    models = torch.nn.Sequential(
        torch.nn.Linear(input_data, hidden_layer),
        torch.nn.ReLU(),
        torch.nn.Linear(hidden_layer, output_data)
    )

torch.nn.MSELoss类

  • 介绍：

    使用均方误差函数对损失值进行计算，定义类的对象时不用传入任何参数，但在使用实例时需要输入两个维度一样的参数方可进行计算

  • 代码：

    1
    2
    3
    4
    5
    loss_f = torch.nn.MSELoss()
    x = Variable(torch.randn(100, 100))
    y = Variable(torch.randn(100, 100))
    loss = loss_f(x, y)
    print(loss.data)

使用损失函数的神经网络

  • 代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    loss_f = torch.nn.MSELoss()

    batch_n = 100
    input_data = 1000
    hidden_layer = 100
    output_data = 10
    epoch_n = 10000
    lr = 1e-6

    x = Variable(torch.randn(batch_n, input_data), requires_grad=False)
    y = Variable(torch.randn(batch_n, output_data), requires_grad=False)

    models = torch.nn.Sequential(
        torch.nn.Linear(input_data, hidden_layer),
        torch.nn.ReLU(),
        torch.nn.Linear(hidden_layer, output_data)
    )

    for epoch in range (epoch_n):
        y_pred = models(x)
        loss = loss_f(y_pred, y)
        if epoch % 1000 == 0:
            print("epoch:{},loss:{:.4f},".format(epoch, loss.data))
        models.zero_grad()
        loss.backward()

        for param in models.parameters():
            param.data -= param.grad.data * lr

torch.optim包

提供非常多的可实现参数自动优化的类，如SGD、AdaGrad、RMSProp、Adam等

使用自动优化的类实现神经网络：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
batch_n = 100  # 一个批次输入数据的数量
hidden_layer = 100
input_data = 1000  # 每个数据的特征为1000
output_data = 10

x = Variable(torch.randn(batch_n, input_data), requires_grad=False)
y = Variable(torch.randn(batch_n, output_data), requires_grad=False)
# 用Variable对Tensor数据类型变量进行封装的操作。requires_grad如果是F，表示该变量在进行自动梯度计算的过程中不会保留梯度值。

models = torch.nn.Sequential(
    torch.nn.Linear(input_data, hidden_layer),
    torch.nn.ReLU(),
    torch.nn.Linear(hidden_layer, output_data)
)
# torch.nn.Sequential括号内就是我们搭建的神经网络模型的具体结构，Linear完成从隐藏层到输出层的线性变换，再用ReLU激活函数激活
# torch.nn.Sequential类是torch.nn中的一种序列容器，通过在容器中嵌套各种实现神经网络模型的搭建，
# 最主要的是，参数会按照我们定义好的序列自动传递下去。


epoch_n = 10000
lr = 1e-4
loss_fn = torch.nn.MSELoss()

optimzer = torch.optim.Adam(models.parameters(), lr=lr)
# 使用torch.optim.Adam类作为我们模型参数的优化函数，这里输入的是：被优化的参数和学习率的初始值。
# 因为我们需要优化的是模型中的全部参数，所以传递的参数是models.parameters()

# 进行模型训练的代码如下：
for epoch in range(epoch_n):
    y_pred = models(x)
    loss = loss_fn(y_pred, y)
    print("Epoch:{},Loss:{:.4f}".format(epoch, loss.data))
    optimzer.zero_grad()  # 将模型参数的梯度归0

    loss.backward()
    optimzer.step()  # 使用计算得到的梯度值对各个节点的参数进行梯度更新。

实例：预测房价

根据历史数据预测未来的房价，实现一个线性回归模型，并用梯度下降算法求解该模型，从而给出预测直线、
求解步骤：准备数据、设计模型、训练和预测

1.准备数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

x = torch.linspace(0, 100, 100).type(torch.FloatTensor)  # time
rand = torch.randn(100) * 10  # noise
y = x + rand  # got history price

x_train = x[: -10]  # training data, get the data except last 10 from x
x_test = x[-10:]  # test data, get the last 10 data from x
y_train = y[: -10]  # train data
y_test = y[-10:]

'''
对训练数据点进行可视化
'''
import matplotlib.pyplot as plt  # 导入画图的程序包

# plt.figure(figsize=(10, 8))  # 设置绘制窗口的大小为10*8 inch

'''
绘制数据，由于x和y都是自动微分变量，因此需要用data获取它们包裹的tensor，并转成numpy
'''
# plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'o')
# plt.xlabel('X')  # 添加X轴的标注
# plt.ylabel('Y')  # 添加Y轴的标注
# plt.show()  # 画图

2.设计模型

  • ​ 希望的到一条尽可能从中间穿越这些数据散点的拟合直线
  • ​ 损失函数
  • ​ 梯度下降
  • ​ 学习率

3.训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 定义随机的a b （线性方程的两个参数，斜率和偏置）
a = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)

# 设置学习率
learning_rate = 0.0001

# 对a和b进行迭代计算
for i in range(1000):
# 计算在当前ab条件下的模型预测值
    # 将所有的训练数据带入模型ax+b,计算每个的预测值
    predictions = a.expand_as(x_train) * x_train + b.expand_as(x_train)
    loss = torch.mean((predictions - y_train)**2)  # 计算预测值和真实值的损失值
    print("loss:{}".format(loss))
    loss.backward()  # 对损失函数进行梯度反传
    # 利用上一步计算中得到的a的梯度信息更新a中的data的数值
    a.data.add_(- learning_rate * a.grad.data)
    # 利用上一步计算中得到的b的梯度信息更新b中的data数值
    b.data.add_(- learning_rate * b.grad.data)
    # 清空存储在变量a、b中的梯度信息，以免在backward的过程中反复不停地累加
    # 不能直接对自动微分变量进行数值更新，只能对它的data属性进行更新
    a.grad.data.zero_()
    b.grad.data.zero_()

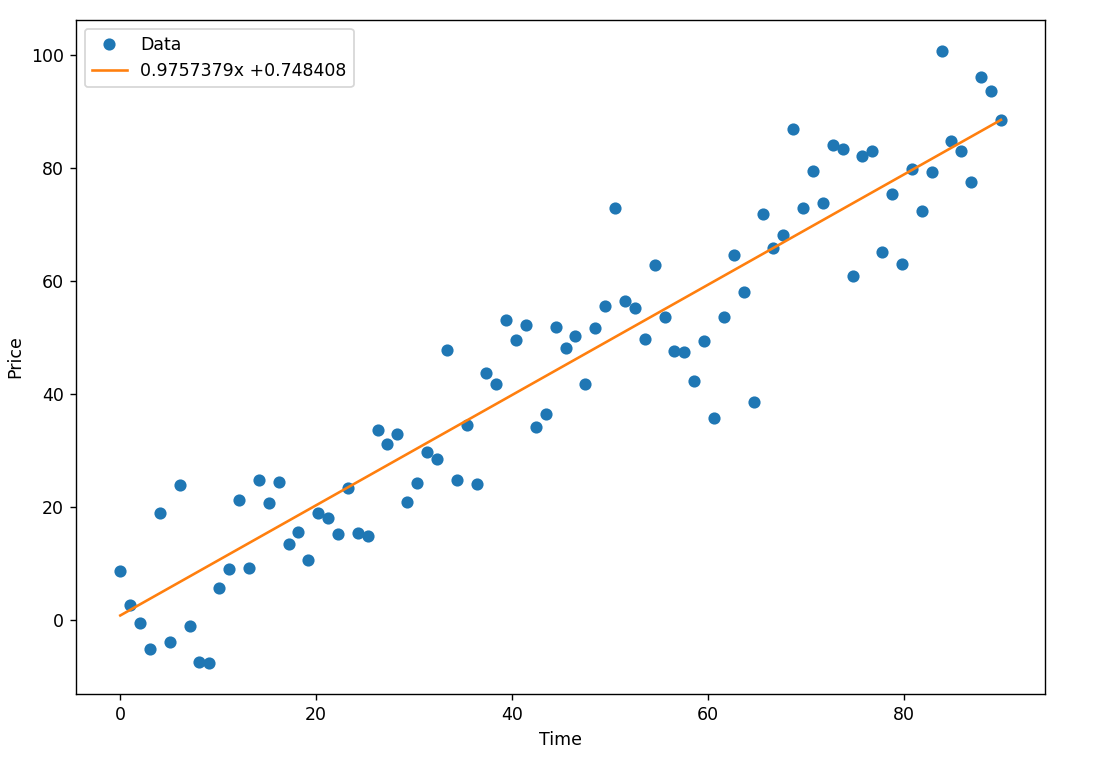
4.画出拟合直线

1
2
3
4
5
6
7
8
9
x_data = x_train.data.numpy()  # 将x中的数据转换成numpy数组
plt.figure(figsize=(10, 7))
xplot, = plt.plot(x_data, y_train.data.numpy(), 'o')  # 绘制x,y 的散点图
yplot, = plt.plot(x_data, a.data.numpy() * x_data + b.data.numpy())  # 绘制直线
plt.xlabel('Time')
plt.ylabel('Price')
str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0])  # 写出表达式
plt.legend([xplot, yplot], ['Data', str1])
plt.show()

效果如下：

5.模型预测

1
2
3
4
5
6
7
8
9
10
11
12
13
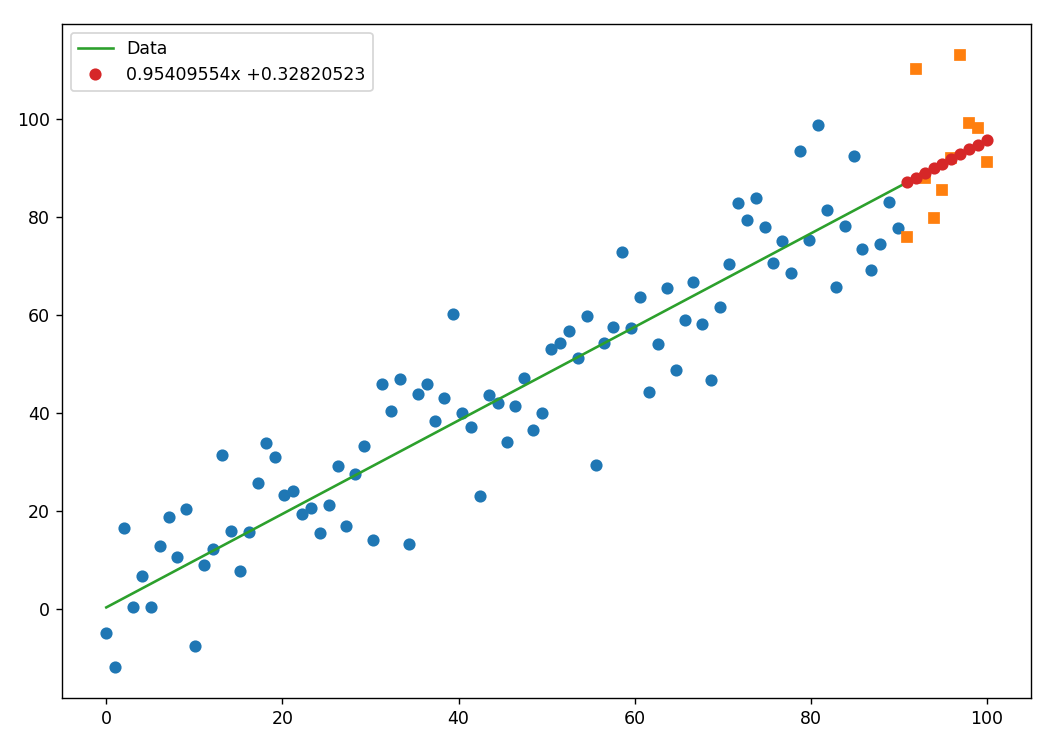
14
predictions = a.expand_as(x_test) * x_test + b.expand_as(x_test)
print(predictions)

x_data = x_train.data.numpy()
x_pred = x_test.data.numpy()
plt.figure(figsize=(10, 7))
plt.plot(x_data, y_train.data.numpy(), 'o')
plt.plot(x_pred, y_test.data.numpy(), 's')
x_data = np.r_[x_data, x_test.data.numpy()]
xplot, = plt.plot(x_data, a.data.numpy() * x_data + b.data.numpy())  # 绘制拟合数据
yplot, = plt.plot(x_pred, a.data.numpy() * x_pred + b.data.numpy(), 'o')  # 绘制预测数据
str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0])  # 写出表达式
plt.legend([xplot, yplot], ['Data', str1])
plt.show()

效果如下：

单车预测器

1.0：使用时间变量x作为自变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
import inline
import matplotlib
import numpy as np
import pandas as pd
import torch
import torch.optim as optim
import matplotlib.pyplot as plt

# 直接在Notebook中显示输出图像

data_path = 'hour.csv'  # 读取数据
rides = pd.read_csv(data_path)  # rides是一个dataframe对象
rides.head()  # 输出部分数据
counts = rides['cnt'][:50]  # 截取数据
x = np.arange(len(counts))  # 获取变量x
y = np.array(counts)  # 单车数量为y
plt.figure(figsize=(10, 7))  # 设定窗口大小
plt.plot(x, y, 'o-')  # 绘制原始数据
plt.xlabel('X')
plt.ylabel('Y')

'''
定义变量，通过这些变量的运算让Pytorch自动生成计算图
'''
# x = torch.FloatTensor(np.arange(len(counts), dtype=float))

# 对x 进行归一化处理
x = torch.FloatTensor(np.arange(len(counts), dtype=float))/len(counts)
y = torch.FloatTensor(np.array(counts, dtype=float))


sz = 10  # 隐含神经元的数量
weights = torch.randn((1, sz), requires_grad=True)  # 从输入层到隐含层的权重向量
biases = torch.randn(sz, requires_grad=True)  # 隐含层的偏置向量
weights2 = torch.randn((sz, 1), requires_grad=True)  # 从隐含层到输出层的权重向量

'''
训练神经网络
'''
learning_rate = 0.001  # 学习率
losses = []  # 该数组用于记录每一次迭代的损失函数值
x = x.view(50, -1)  # 重新设置shape -1表示自动设置
y = y.view(50, -1)
for i in range(100000):
    hidden = x * weights + biases  # 隐含层
    # 此时hidden的尺寸时50，10，即50个数据点，10个神经单元

    # 将sigmoid函数运用在每个隐含层的神经元上
    hidden = torch.sigmoid(hidden)
    # 隐含层输出到输出层，得到最终预测结果
    predictions = hidden.mm(weights2)  # 此时predications的尺寸为50,1
    # 计算Loss
    loss = torch.mean((predictions - y)**2)
    losses.append(loss.data.numpy())
    if i % 10000 == 0:
        print("loss:{}".format(loss))

    # 执行梯度下降算法，反向传播误差
    loss.backward()
    # 更新参数
    weights.data.add_(- learning_rate * weights.grad.data)
    biases.data.add_(- learning_rate * biases.grad.data)
    weights2.data.add_(- learning_rate * weights2.grad.data)

    # 清空所有的梯度值
    weights.grad.data.zero_()
    biases.grad.data.zero_()
    weights2.grad.data.zero_()

# 查看Loss值的下降过程
# plt.plot(losses)
# plt.xlabel('Epoch')
# plt.ylabel('Loss')
# plt.show()

'''
绘制50个数据点的预测曲线
'''
# x_data = x.data.numpy()
# plt.figure(figsize=(10, 7))
# xplot, = plt.plot(x_data, y.data.numpy(), 'o')  # 绘制原始数据
# yplot, = plt.plot(x_data, predictions.data.numpy())  # 绘制拟合曲线
# plt.xlabel('X')
# plt.ylabel('Y')
# plt.legend([xplot, yplot], ['Data', 'Prediction under 1000000 epochs'])
# plt.show()

'''
用训练好的模型来做预测
:由于训练时产生了过拟合的问题，所以预测数据域真实数据的差距很大
'''
counts_predict = rides['cnt'][50:100]
x = torch.FloatTensor((np.arange(len(counts_predict), dtype=float) + len(counts)) / len(counts))  # 归一化后的测试数据
y = torch.FloatTensor(np.array(counts_predict, dtype=float))

# 用x预测y
hidden = x.expand(sz, len(x)).t() * weights.expand(len(x), sz)  # 从输入层到隐含层的计算
hidden = torch.sigmoid(hidden)  # 将sigmoid函数应用在每一个神经元上
predictions = hidden.mm(weights2)
loss = torch.mean((predictions - y)**2)
print(loss)

x_data = x.data.numpy()
plt.figure(figsize=(10,7))
xplot, = plt.plot(x_data, y.data.numpy(), 'o')
yplot, = plt.plot(x_data, predictions.data.numpy())
plt.xlabel('X')
plt.ylabel('Y')
plt.legend([xplot, yplot], ['data', 'prediction'])
plt.show()
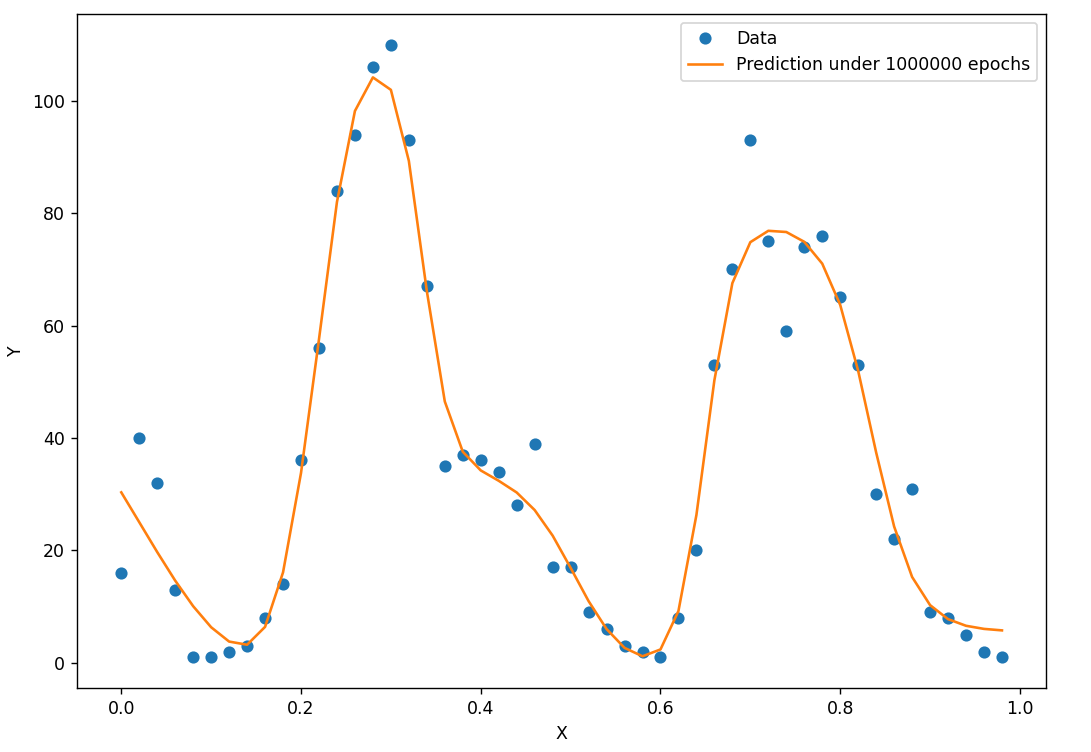
训练效果

数据拟合曲线：

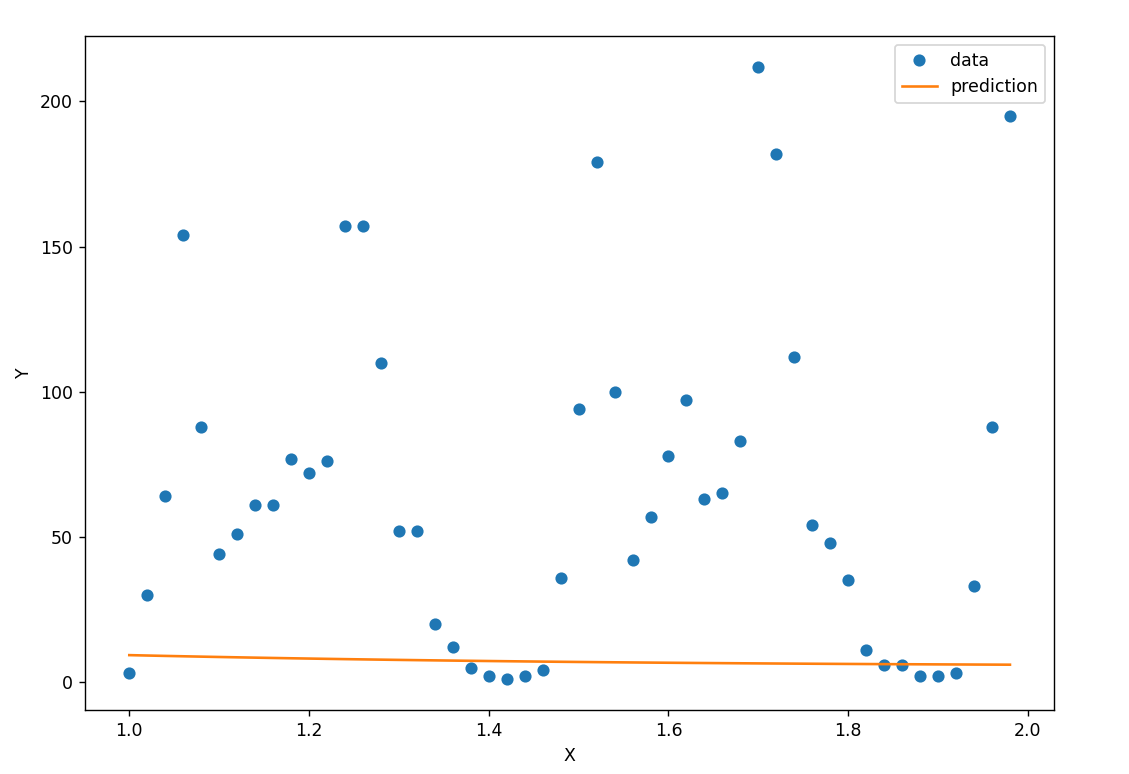
预测效果： 由于使用的自变量x和Y之间不存在依赖关系，得到的模型完全失能

预测曲线如下：

2.0 使用相关数据预测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
'''
单车预测器2.0!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
'''

'''
数据预处理
1.对分类类型变量的onehot编码
2.对数值类型变量的处理
'''
# 对类型编码变量的处理
data_path = 'hour.csv'  # 读取数据
rides = pd.read_csv(data_path)  # rides是一个dataframe对象
rides.head()  # 输出部分数据
counts = rides['cnt'][:50]  # 截取数据
dummy_fields = ['season', 'weathersit', 'mnth', 'hr', 'weekday']  # 所有类型变量的名称
for each in dummy_fields:
    # 取出所有类型变量，将它们转换为独热编码
    dummies = pd.get_dummies(rides[each], prefix=each, drop_first=False)
    # 将新的独热编码与原有所有变量合并
    rides = pd.concat([rides, dummies], axis=1)

# 将原来的类型变量从数据表中删除
fields_to_drop = ['instant', 'dteday', 'season', 'weathersit', 'weekday', 'atemp', 'mnth', 'workingday',
                  'hr']  # 要删除的类型的名称
data = rides.drop(fields_to_drop, axis=1)  # 删除

# 对数值编码变量的处理  :对变量进行标准化（标准正态分布）
quant_features = ['cnt', 'temp', 'hum', 'windspeed']  # 数值变量名称
scaled_features = {}  # 将每一个变量的均值和方差都存储到scaled_features变量中
for each in quant_features:
    mean, std = data[each].mean(), data[each].std()
    scaled_features[each] = [mean, std]
    # 对每个变量进行标准化
    data.loc[:, each] = (data[each] - mean) / std

# 数据集的划分

test_data = data[-21 * 24:]
train_data = data[: -21 * 24]

# 目标列包含的字段
target_fields = ['cnt', 'casual', 'registered']

# 将训练集划分成特征变量和目标变量
features, targets = train_data.drop(target_fields, axis=1), train_data[target_fields]

# 将测试数据划分成特征变量和目标变量
test_features = test_data.drop(target_fields, axis=1)
test_targets = test_data[target_fields]

# 将数据类型转换为numpy数组
X = features.values
Y = targets['cnt'].values
X = X.astype(float)
Y = Y.astype(float)

Y = np.reshape(Y, [len(Y), 1])
losses = []

'''
构建神经网络
'''

# 定义神经网络架构， features.shape[1] 个输入单元， 10 个隐含单元， 1个输出单元
input_size = features.shape[1]
hidden_size = 10
output_size = 1
batch_size = 128
neu = torch.nn.Sequential(
    torch.nn.Linear(input_size, hidden_size),
    torch.nn.Sigmoid(),
    torch.nn.Linear(hidden_size, output_size),
)

cost = torch.nn.MSELoss()
optimizer = torch.optim.SGD(neu.parameters(), lr=0.01)

# 训练

for i in range(1000):
    # 每128个样本点划分为一批，在循环的时候一批一批地读取
    batch_loss = []
    # start end 分别是提取一批数据的其实下表和终止下标
    for start in range(0, len(X), batch_size):
        end = start + batch_size if start + batch_size < len(X) else len(X)
        xx = torch.tensor(X[start:end], dtype=torch.float, requires_grad=True)
        yy = torch.tensor(Y[start:end], dtype=torch.float, requires_grad=True)
        predict = neu(xx)
        loss = cost(predict, yy)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        batch_loss.append(loss.data.numpy())
    # 每隔100步输出损失值
    if i % 100 == 0:
        losses.append(np.mean(batch_loss))
        print(i, np.mean(batch_loss))

plt.plot(np.arange(len(losses)) * 100, losses)
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.show()

'''
测试神经网络
'''

# 用训练好的神经网络在测试集上进行预测
targets = test_targets['cnt']  # 读取测试集的cnt数值
targets = targets.values.reshape([len(targets), 1])  # 将数据转换成合适的tensor形式
targets = targets.astype(float)  # 保证数据为实数

x = torch.tensor(test_features.values.astype(float), dtype=torch.float, requires_grad=True)
y = torch.tensor(targets.astype(float), dtype=torch.float, requires_grad=True)

print(x[:10])
# 用神经网络进行预测
predict = neu(x)
predict = predict.data.numpy()

print((predict * std + mean)[:10])

# 将后21天的预测数据与真实数据画在一起并比较
# 横坐标轴是不同的日期，纵坐标轴是预测或者真实数据的值
fig, ax = plt.subplots(figsize=(10, 7))

mean, std = scaled_features['cnt']
ax.plot(predict * std + mean, label='Prediction', linestyle='--')
ax.plot(targets * std + mean, label='Data', linestyle='-')
ax.legend()
ax.set_xlabel('Date-time')
ax.set_ylabel('Counts')
# 对横坐标轴进行标注
dates = pd.to_datetime(rides.loc[test_data.index]['dteday'])
dates = dates.apply(lambda d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24], rotation=45)

中文情绪分类器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227

'''
搭建简单的文本分类器
'''
import re
from collections import Counter

import jieba
import numpy as np
import torch
from torch import nn

'''
数据处理
'''
# 导入数据
good_file = 'data/good.txt'
bad_file = 'data/bad.txt'


# 1.过滤标点符号
def filter_punc(sentence):
    sentence = re.sub("[\s+\.\!\/_,$%^*(+\"\'“”《》?“]+|[+——！，。？、~@#￥%……&*（）：]+", "", sentence)
    return sentence


# 2.分词
# 扫描所有的文本，分词并建立词典，分出正面还是负面的评论，is_filter可以过滤标点符号
def Prepare_data(good_file, bad_file, is_filter=True):
    all_words = []  # 存储所有的单词
    pos_sentences = []  # 存储正面评论
    neg_sentences = []  # 存储负面评论
    with open(good_file, 'r', encoding='utf-8') as fr:
        for idx, line in enumerate(fr):
            if is_filter:
                # 过滤标点符号
                line = filter_punc(line)
                # 分词
                words = jieba.lcut(line)
            if len(words) > 0:
                all_words += words
                pos_sentences.append(words)
    print('{0} 包含 {1}行，{2} 个单词。'.format(good_file, idx + 1, len(all_words)))

    count = len(all_words)
    with open(bad_file, 'r', encoding='utf-8') as fr:
        for idx, line in enumerate(fr):
            if is_filter:
                line = filter_punc(line)
                words = jieba.lcut(line)

            if len(words) > 0:
                all_words += words
                neg_sentences.append(words)
    print('{0} 包含 {1}行，{2} 个单词。'.format(good_file, idx + 1, len(all_words)))

    # 3.建立单词表 每一项与{w:[id,freq]}

    diction = {}
    cnt = Counter(all_words)
    for word, freq in cnt.items():
        diction[word] = [len(diction), freq]
    print('字典大小：{0}'.format(len(diction)))
    return pos_sentences, neg_sentences, diction


# 调用Prepare_data, 完成数据处理工作
pos_sentences, neg_sentences, diction = Prepare_data(good_file, bad_file, True)
st = sorted([(v[1], w) for w, v in diction.items()])


# 查找单词的编码
def word2index(word, diction):
    if word in diction:
        value = diction[word][0]
    else:
        value = -1
    return value


# 根据编码获取单词
def index2word(index, diction):
    for w, v in diction.items():
        if v[0] == index:
            return w
    return None


'''
文本数据向量化
'''


# 输入一个句子和相应的词典，得到这个句子的向量化表示
# 向量的尺寸为词典中单词的数量，向量中位置i的值表示第i个单词在sentence中出现的频率
def sentence2vec(sentence, dictionary):
    vector = np.zeros(len(dictionary))
    for l in sentence:
        vector[l] += 1
    return 1.0 * vector / len(sentence)


# 遍历所有句子，将每一个单词映射成编码
dataset = []  # 数据集
labels = []  # 标签
sentences = []  # 原始句子

# 处理正面评论
for sentence in pos_sentences:
    new_sentence = []
    for l in sentence:
        if l in diction:
            new_sentence.append(word2index(l, diction))
    dataset.append(sentence2vec(new_sentence, diction))
    labels.append(0)  # 正标签为0
    sentences.append(sentence)

# 处理负向评论
for sentence in neg_sentences:
    new_sentence = []
    for l in sentence:
        if l in diction:
            new_sentence.append(word2index(l, diction))
    dataset.append(sentence2vec(new_sentence, diction))
    labels.append(1)  # 负标签为1
    sentences.append(sentence)
# 打乱所有数据的顺序，形成数据集
# indices 为所有数据下标的排列
indices = np.random.permutation(len(dataset))
# 根据打乱的下标，重新生成数据集dataset,标签集labels, 以及对应的原始句子sentences
dataset = [dataset[i] for i in indices]
labels = [labels[i] for i in indices]
sentences = [sentences[i] for i in indices]

# 划分数据集
test_size = int(len(dataset) // 10)
train_data = dataset[2 * test_size:]
train_label = labels[: test_size]

valid_data = dataset[: test_size]
valid_label = labels[: test_size]

test_data = dataset[test_size: 2 * test_size]
test_label = labels[test_size: 2 * test_size]

'''
建立神经网络
'''
# 一个简单的前馈神经网络，共三层
# 第一层为线性层， 加一个非线性relu, 第二层为线性层， 中间有10个隐含单元

# 输入维度是词典的大小，每一条评论的词袋模型
model = torch.nn.Sequential(
    nn.Linear(len(diction), 10),
    nn.ReLU(),
    nn.Linear(10, 2),
    nn.LogSoftmax(dim=1)
)


# 自定义的计算一组数据分类准确率的函数
# predictions 为模型给出的预测结果，labels 为数据中的标签， 比较二者已确定整个神经网络当前的表现
def rightness(predictions, labels):
    """计算预测错误率的函数，其中predictions是模型给出的一组预测结果，batch_size行num_classes列的矩阵，labels是数据之中的正确答案"""
    pred = torch.max(predictions.data, 1)[1]  # 对于任意一行（一个样本）的输出值的第1个维度，求最大，得到每一行的最大元素的下标
    rights = pred.eq(labels.data.view_as(pred)).sum()  # 将下标与labels中包含的类别进行比较，并累计得到比较正确的数量
    return rights, len(labels)  # 返回正确的数量和这一次一共比较了多少元素


'''
训练模型
'''
# 损失函数为交叉熵
cost = torch.nn.NLLLoss()
# 优化算法为Adam，可以自动调节学习率
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
records = []

# 循环10个Epoch
losses = []
for epoch in range(10):
    for i, data in enumerate(zip(train_data, train_label)):
        x, y = data

        # 需要将输入的数据进行适当的变形，主要是要多出一个batch_size的维度，也即第一个为1的维度
        x = torch.tensor(x, requires_grad=True, dtype=torch.float).view(1, -1)
        # x的尺寸：batch_size=1, len_dictionary
        # 标签也要加一层外衣以变成1*1的张量
        y = torch.tensor(np.array([y]), dtype=torch.long)
        # y的尺寸：batch_size=1, 1

        # 清空梯度
        optimizer.zero_grad()
        # 模型预测
        predict = model(x)
        # 计算损失函数
        loss = cost(predict, y)
        # 将损失函数数值加入到列表中
        losses.append(loss.data.numpy())
        # 开始进行梯度反传
        loss.backward()
        # 开始对参数进行一步优化
        optimizer.step()

        # 每隔3000步，跑一下校验数据集的数据，输出临时结果
        if i % 3000 == 0:
            val_losses = []
            rights = []
            # 在所有校验数据集上实验
            for j, val in enumerate(zip(valid_data, valid_label)):
                x, y = val
                x = torch.tensor(x, requires_grad=True, dtype=torch.float).view(1, -1)
                y = torch.tensor(np.array([y]), dtype=torch.long)
                predict = model(x)
                # 调用rightness函数计算准确度
                right = rightness(predict, y)
                rights.append(right)
                loss = cost(predict, y)
                val_losses.append(loss.data.numpy())

            # 将校验集合上面的平均准确度计算出来
            right_ratio = 1.0 * np.sum([i[0] for i in rights]) / np.sum([i[1] for i in rights])
            print('第{}轮，训练损失：{:.2f}, 校验损失：{:.2f}, 校验准确率: {:.2f}'.format(epoch, np.mean(losses),
                                                                                       np.mean(val_losses),
                                                                                       right_ratio))
            records.append([np.mean(losses), np.mean(val_losses), right_ratio])

卷积神经网络

实现手写数字识别
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
# _*_ coding : utf-8_*_
# @Time : 2023/7/10 15:39 
# @Author : Chengwei
# @File : minist
# @Project : local

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.utils.data

import torchvision.datasets as dsets
import torchvision.transforms as transforms

import matplotlib.pyplot as plt
import numpy as np


'''
数据准备
'''
# 定义一些训练用的超参数
image_size = 28  # 图像的总尺寸为28x28
num_classes = 10  # 标签的种类数
num_epochs = 20  # 训练的总循环周期
batch_size = 64  # 一个批次的大小，64张图片

# 加载MNIST数据，如果没有下载过，系统就会在当前路径下进件/data目录，便把文件存放在其中
# MNIST数据是torchvision包自带的，可以直接调用
# 当用户想调用自己的图像数据时，可以用torchvision.datasets.ImageFolder
# 或torch.utils.data.TensorDataset来加载

#加载训练集
train_dataset = dsets.MNIST(
    root='./data',  # 文件存放的路径
    train=True,  # 提取训练集
    #将图像转化为张量，在加载数据时，就可以对图像做预处理
    transform=transforms.ToTensor(),
    download=True  # 找不到文件时，自动下载
)

# 加载测试集
test_dataset = dsets.MNIST(
    root='./data',
    train=False,
    transform=transforms.ToTensor()
)

# 训练集的加载器，自动将数据切分成批，顺序随机打乱
train_loader = torch.utils.data.DataLoader(
    dataset=train_dataset,
    batch_size=batch_size,
    shuffle=True
)
# 我们希望将测试数据分成两部分，一部分作为校验数据，另一部分作为测试数据

#定义下标数组indices,相当于对所有test_dataset中数据的编码
#然后，定义下标Indices_val表示校验集数据的下标，indices_test表示测试集的下标
indices = range(len(test_dataset))
indices_val = indices[:5000]
indices_test = indices[5000:]

#根据下标构造两个数据集的SubsetRandomSampler采样器，它会对下标进行采样
sampler_val = torch.utils.data.sampler.SubsetRandomSampler(indices_val)
sampler_test = torch.utils.data.sampler.SubsetRandomSampler(indices_test)

# 根据两个采样器定义加载器
validation_loader = torch.utils.data.DataLoader(
    dataset=test_dataset,
    batch_size=batch_size,
    shuffle=False,
    sampler=sampler_val
)
test_loader = torch.utils.data.DataLoader(
    dataset=test_dataset,
    batch_size=batch_size,
    shuffle=False,
    sampler=sampler_test
)

# 随便从数据集中读入一张图片，并绘制出来
idx = 100

# dataset支持下标索引，其中提取出来的元素为features,target格式，即属性和标签
# [0]表示索引features
muteimg = train_dataset[idx][0].numpy()
#一般的图像包含RGB三个通道，而MNIST数据集的图像都是灰度的，只有一个通道
#因此，我们忽略通道，把图像看做一个灰度矩阵
#用imshow画图，会将灰度矩阵自动展现为彩色，不同灰度对应不同的颜色，从黄到紫
plt.imshow(muteimg[0,...])
print('标签是：',train_dataset[idx][1])


'''
构建网络
'''

#定义卷积神经网络：4和8是人为指定的两个卷积层的厚度（feature map的数量)
depth = [4, 8]
class ConvNet(nn.Module):
    def __init__(self):
        # 构造函数 该函数在创建一个ConvNet对象时会被执行
        # 首先调用父类响应的构造函数
        super(ConvNet, self).__init__()
        #其次构造ConvNet需要用到的各个神经模块
        #定义组件并不是真正搭建组建，只是把基本建筑砖块找好
        #定义一个卷积层，输入通道为1，输出通道为4，窗口大小为5，padding为2
        self.conv1 = nn.Conv2d(1, 4, 5, padding=2)
        self.pool = nn.MaxPool2d(2, 2)  # 定义一个池化层，一个窗口为2x2的池化运算
        # 第二层卷积，输入通道为depth[0],输出通道为depth[1], 窗口为5，padding 为2
        self.conv2 = nn.Conv2d(depth[0], depth[1], 5, padding=2)
        # 一个线性连接层，输入尺寸为最后一次立方体的线性平铺，输出层为512个结点
        self.fc1 = nn.Linear(image_size // 4 * image_size // 4 * depth[1], 512)
        self.fc2 = nn.Linear(512, num_classes)  # 最后一层线性分类单元，输入为512，输出为要分类的类别数

    def forward(self, x):
        # 该函数完成神经网络真正的前向运算，在这里把各个组件进行实际的拼装
        # x的尺寸：(batch_size, image_channels, image_width, image_height)
        x = self.conv1(x)  # 第一层卷积
        x = F.relu(x)  # 激活函数用relu,防止 过拟合
        # x 的尺寸：(batch_size, num_filters, imge_width, image_height)

        x = self.pool(x)  # 第二层池化，将图片缩小
        #x的尺寸：(batch_size,depth[0],image_width/2,image_height/2)

        x = self.conv2(x)  # 第三层卷积，窗口为5，输入输出通道分别为depth[0]=4,depth[1]=8
        x = F.relu(x)  # 非线性函数
        # x的尺寸：(batch_size,depth[1],image_width/2,image_height/2)
        
        x = self.pool(x)  # 第四层池化，将图片缩小为原来的1/4
        #  x的尺寸：(batch_size, depth[1], image_width/4,image_height/4)
        
        # 将立体图的特征图tensor压成一个一维的向量
        # view() 函数可以将一个tensor按指定方式重新排布
        x = x.view(-1, image_size // 4 * image_size // 4 * depth[1])
        # x的尺寸：(batch_size, depth[1] * image_width/4*image_height/4)
        
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        #x的尺寸：(batch_size,num_classes)
        
        #输出层为 log_softmax,即概率对数值log(p(x))
        # 使用log_softmax可以是后面的交叉熵计算更快
        x = F.log_softmax(x, dim=1)
        return x
    def retrieve_features(self, x):
        #该函数用于提取卷积神经网络的特征图，返回feature_map1
        #feature_map2为前两层卷积层的特征图
        feature_map1 = F.relu(self.conv1(x))
        x = self.pool(feature_map1)
        feature_map2 = F.relu(self.conv2())
        return feature_map1, feature_map2

注：由于博客篇幅过长，后续的模块可能会单独写一个博客总结。详见分类——机器学习

欢迎关注我的其它发布渠道